
The Number 2,187
Is Lucky. Here's Why:
It has a host of surprising properties, although it is not necessarily "lucky" in the usual sense of the word
In remembering Martin Gardner - (Martin Gardner's Lucky Numbers archived on Wikiwix.com) - on what would have been his 100th birthday this month, we recalled a 1997 article he wrote for The Mathematical Intelligencer. In that piece he asks his imaginary friend Dr. Irving Joshua Matrix-"the world's most famous numerologist" and a recurring character in his Scientific American Mathematical Games column-about 2187, the house number of Gardner's childhood home in Tulsa, Okla. Dr. Matrix instantly regales Gardner with a raft of facts about the number 2,187. It is 3 raised to the power of 7 and 10,000,000 written in base 3 notation; subtract 2,187 from 9,999 and you get 7,812, its reversal; multiply 21 by 87 to yield 1,827, or 27 by 81 to get 2,187 again. "Every number has endless unusual properties," Dr. Matrix comments, adding that 2,187 is also a lucky number.
back to the menu
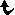
Lucky numbers are distant cousins of prime numbers, those divisible only by themselves and 1. Although different in many ways, both can be generated using what are known as sieves. Greek mathematician Eratosthenes devised a famous sieve for sifting out primes from the positive integers in counting order: First cross out all multiples of 2, except for 2, then cross out all multiples of 3, then 5, 7, 11 and so forth. Carry on to infinity and you will be left with a pile of all the primes. Polish-American mathematician Stanislaw Ulam came up with another sort of sieve in the mid-1950s: Again starting with the positive integers in counting order, cross out every second number, leaving the odd ones. The second surviving number is then 3; so cross out every third number not yet eliminated. The third surviving number is then 7; so cross out every 7th integer. The fourth survivor at this point is 9; so eliminate every 9th integer and keep going. Ultimately certain numbers forever escape the sieve, which is why Ulam called them lucky.
Lucky and prime numbers share some curious sieve-family traits. For instance, there are 25 primes and 23 luckies less than 100 and there are eight twin primes (which differ only by two) and seven twin luckies less than 100. One of the most famous unsolved problems involving primes is Goldbach's conjecture, which states that every even number greater than 2 can be expressed as the sum of two primes. Also unsolved is the similar proposition that every even number is the sum of two lucky numbers.
back to the menu
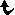
Here's another interesting fact about 2,187-the sums to the right of the equal signs below area all permutations of the numbers that were added to 2,187 on the left.
- 2187 + 1234= 3421
- 2187 + 12345 = 14532
- 2187 + 123456 = 125643
- 2187 + 1234567 = 1236754
- 2187 + 12345678 = 12347865
- 2187 + 123456789 = 123458976
Known as one of the most generous lotteries in United Kingdom: National Lottery UK! It runs all Wednesday and Saturdays. You can become a winner of glorious jackpots! The most attractive ones start at 12 millions, rolling over each week if there are no winners. Only three Jackpot rollovers are accepted. One rollover is frequent, but three consecutive rollovers have only occured four times in the history of the National Lottery. In the UK National Lottery, 6 numbers are drawn from a range between 1 and 49, plus a bonus ball. Players who hit three or more numbers have a chance to win a prize! Players who hit all six numbers win the jackpot. The bonus ball is only useful for those who hit five of the six winning numbers. Those players who guessed five numbers and the bonus ball receive a bigger prize than those who only hit five numbers. When there is more than one winner at a level of prizes, money is divided among all winners. Don't miss this opportunity.
Play now!
back to the MENU
© Copyright 2000
Contact
Disclaimer - Privacy